Решите систему: 
Решение. Рассмотрим первое неравенство системы. Ограничения на 
Разложим на множители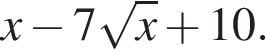 
Ясно, что 
При 
и 
левая часть неравенства будет иметь вид: 
а само неравенство — 
Тогда:
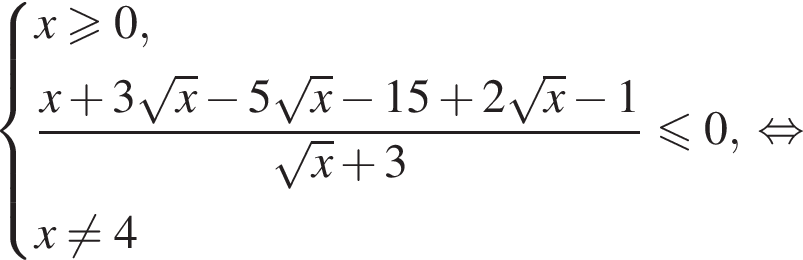
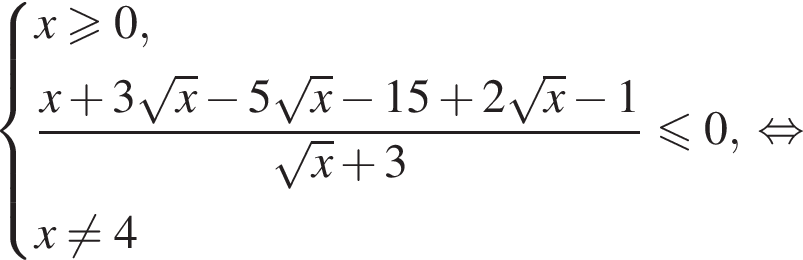
Итак, решениями первого неравенства системы является множество 
Теперь рассмотрим второе неравенство системы. Обратим внимание на то, что числители левой и правой частей равны. Следовательно, знак равенство между левой и правой частями нестрогого неравенства выполняется только при выполнении условия 
т. е. при 
или 
Но с учетом результата, полученного при решении первого неравенства, рассмотрение значения можно исключить. Таким образом, 
– это часть решения второго неравенства системы.
Теперь потребуем, чтобы выражение 
было неположительным. Ясно, что это условие будет выполнено при 
Но с учетом решений первого неравенства, второе неравенство можно рассмотреть только на множестве [0; 5]. В таком случае нам остается решить неравенство 
Ответ: 
| Критерии оценивания выполнения задания | Баллы |
|---|---|
| Обоснованно получен верный ответ. | 3 |
| Обоснованно получены верные ответы в обоих неравенствах исходной системы. | 2 |
| Обоснованно получен верный ответ в одном неравенстве исходной системы. ИЛИ получен неверный ответ из-за вычислительной ошибки, но при этом имеется верная последовательность всех шагов решения системы неравенств. | 1 |
| Решение не соответствует ни одному из критериев, перечисленных выше. | 0 |
| Максимальный балл | 3 |