Решите систему 
Решение. Решим первое неравенство системы. Подмодульные выражения обращаются в нуль в точках: 
Разобъем числовую прямую на промежутки: 
и определим знаки подмодульных выражений на каждом из этих промежутков.
1. Пусть 
Тогда все подмодульные выражения будут неположительными. Неравенство примет вид:
На рассматриваемом промежутке найдется единственная точка, удовлетворяющая неравенству: 
2. Пусть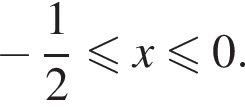 
Тогда
На рассматриваемом промежутке получим: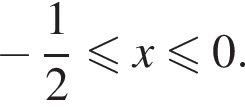
3. Пусть 
Тогда
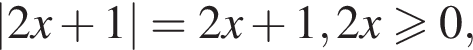
На рассматриваемом промежутке:
4. Пусть 
Тогда
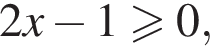
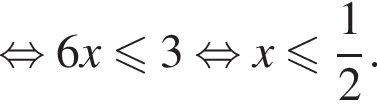
На рассматриваемом промежутке: 
Таким образом, решения первого неравенства системы есть отрезок 
Теперь будем искать решения второго неравенства системы:
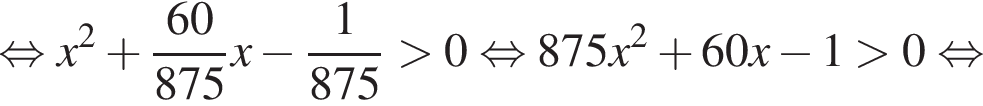
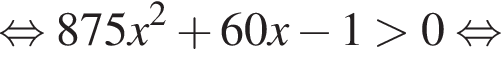
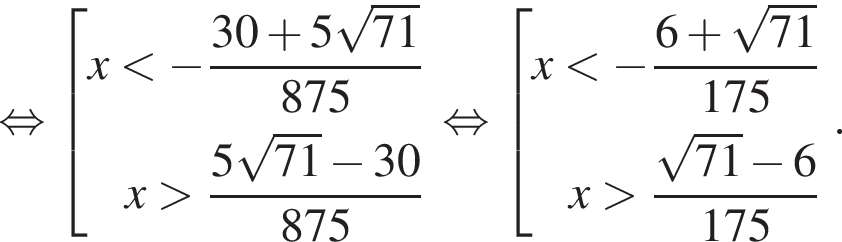
Итак, решения второго неравенства системы: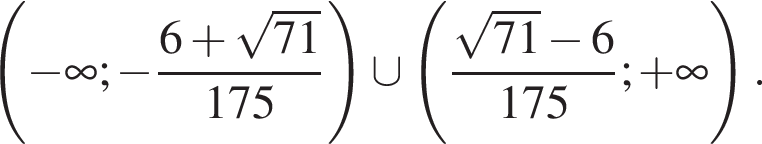 
Сравним числа: 
и 
и 
(неравенство верно, так как 
).
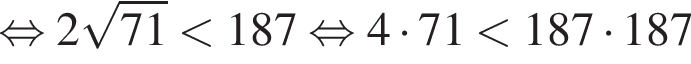(неравенство верно).
Пересечём решения обоих неравенств: 
Ответ: 
| Критерии оценивания выполнения задания | Баллы |
|---|---|
| Обоснованно получен верный ответ. | 3 |
| Обоснованно получены верные ответы в обоих неравенствах исходной системы. | 2 |
| Обоснованно получен верный ответ в одном неравенстве исходной системы. ИЛИ получен неверный ответ из-за вычислительной ошибки, но при этом имеется верная последовательность всех шагов решения системы неравенств. | 1 |
| Решение не соответствует ни одному из критериев, перечисленных выше. | 0 |
| Максимальный балл | 3 |