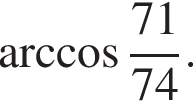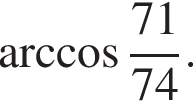Дана правильная треугольная призма 
, стороны основания которой равны 
Найдите угол между прямыми 
и 
, если сумма длин всех сторон обоих оснований равна 
Решение. Решение:
1) Элементарно-геометрическим методом.
Достроим заданную призму до прямой четырехугольной призмы 
Соединим отрезками точки B и 
и 
Ясно, что 
|| 
— искомый. 
По теореме Пифагора получим: 
Очевидно также, что также 
По теореме косинусов будем иметь:
где 
— искомый угол.
Вычислим 
также по теореме косинусов.
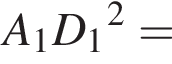
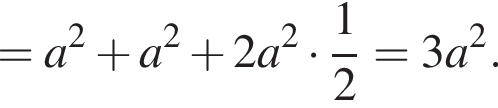
Итак, 
2) Координатно-векторным методом.
Пусть 
— искомый угол. Тогда 
Введем декартову систему координат (см.рисунок). Найдем координаты нужных точек:
, 
, 
, 
, 
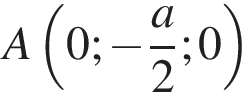Представим векторы 
в координатах: 
, 
Для отыскания угла воспользуемся понятием скалярного произведения двух векторов.
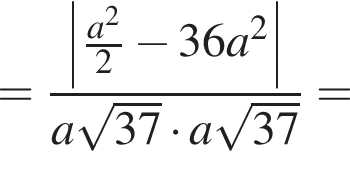
Ответ: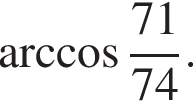 
| Критерии оценивания выполнения задания | Баллы |
|---|---|
| Обоснованно получен верный ответ. | 2 |
| Решение содержит обоснованный переход к планиметрической задаче, но получен неверный ответ или решение не закончено ИЛИ при правильном ответе решение недостаточно обосновано. | 1 |
| Решение не соответствует ни одному из критериев, перечисленных выше. | 0 |