При каких значениях а уравнение
имеет ровно три решения?
Решение. Преобразуем уравнение
Построим эскиз графика функции 
Для этого построим гиперболу 
и отразим часть графика лежащую ниже оси абсцисс в верхнюю полуплоскость. Заметим, что
Значит, асимптотами гиперболы являются прямые 
и 
Графиком функции 
является прямой угол с направленными вниз сторонами и вершиной в точке 
При отрицательных значениях параметра a уравнение не имеет корней (см. левый рисунок). При увеличении значения параметра a, количество корней уравнения будет меняться от нуля до четырёх: сначала один корень, потом два, три и, наконец, четыре. При этом три решения будет только в одном случае, когда луч, задаваемый уравнением 
касается правой ветви гиперболы (см. правый рисунок).
Случай касания прямой и гиперболы соответствует нулевому дискриминанту, получившегося квадратного уравнения:
Значение 
не подходит, та как это случай касания прямой 
и левой ветви гиперболы 
а значение 
подходит. Получаем, что при уравнение имеет три корня.
Ответ:
Укажем идею решения Льва Бреслава.
Заметим, что график функции 
симметричен относительно прямой y = x. Тогда если x0 является корнем уравнения, то 
также является корнем уравнения, поскольку
Следовательно, для того, чтобы количество корней уравнения было нечетным, должно выполняться условие 
откуда 
(тогда a = 2) или 
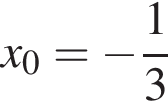(тогда 
). Необходимо проверить найденные значения параметра.
Решив уравнение
получим, что оно имеет ровно 3 решения: 
Решив уравнение 
получим, что оно имеет одно решение: 
Следовательно, подходит значение a = 2.
Приведем другое решение.
Построим график левой части уравнения. Для этого исследуем функцию 
на промежутках 
1. Пусть 
Тогда:
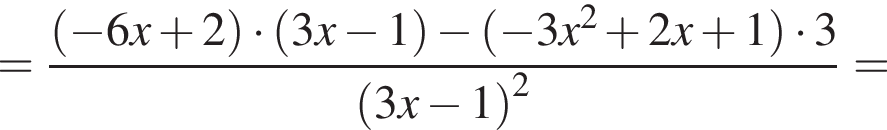
Числитель этой дроби отрицателен при любом значении х, поскольку 
Знаменатель на 
положителен. Следовательно, 
для любого 
А это значит, что критических точек функция на рассматриваемом промежутке не имеет, функция там строго убывающая.
2. Пусть 
Тогда:
Следовательно, при 
при 
А это значит, что при 
функция y убывает, при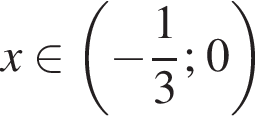 
она возрастает. Точка 
есть точка минимума.
Итак, 
— минимум функции.
3. Пусть 
Тогда:
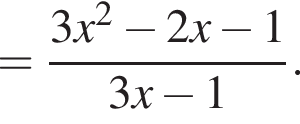
Числитель этой дроби положителен при любом значении х, поскольку Знаменатель также положителен на 
Значит, 
на А это значит, что критических точек функция на рассматриваемом промежутке не имеет, функция там строго возрастающая.
4. Пусть 
Тогда:
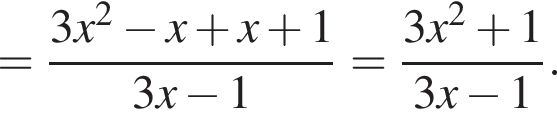
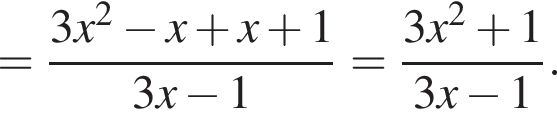
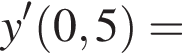
Следовательно, что при 
при 
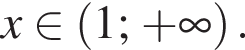А это значит, что при 
функция убывает, при 
она возрастает. Точка 
есть вторая точка минимума.
Таким образом, 2 — второй минимум функции.
Множество значений функции 
нетрудно заметить, есть 
Функция 
постоянная.
Суждения о количестве корней заданного уравнения в зависимости от значений параметра а можно получить исходя из графического представления двух рассмотренных функций (см. ниже).
Ясно, что заданное уравнение:
при 
корней не имеет;
при имеет единственный корень;
при 
имеет ровно два корня;
при имеет ровно три корня;
при 
имеет ровно четыре корня.
Ответ: 2.
| Критерии оценивания выполнения задания | Баллы |
|---|---|
| Обоснованно получен правильный ответ. | 4 |
| С помощью верного рассуждения получено множество значений a, отличающееся от искомого конечным числом точек. | 3 |
| С помощью верного рассуждения получены все граничные точки искомого множества значений a. | 2 |
| Верно найдена хотя бы одна граничная точка искомого множества значений a ИЛИ установлено, что исходное уравнение при всех значениях a имеет единственное решение . | 1 |
| Решение не соответствует ни одному из критериев, перечисленных выше. | 0 |
2. 2.