Найдите все значения а, при каждом из которых уравнение
имеет единственный корень.
Решение. Если 
является корнем исходного уравнения, то и 
является его корнем. Значит, исходное уравнение имеет единственный корень, только если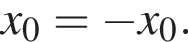 
то есть 
Подставим значение 
в исходное уравнение:
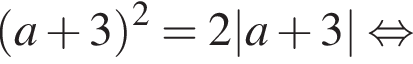
откуда либо 
либо 
или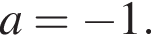 
При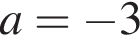 
исходное уравнение принимает вид: 
Корнями этого уравнения являются числа 
и 
то есть исходное уравнение имеет более одного корня.
При 
и при 
уравнение принимает вид: 
При 
это уравнение сводится к уравнению 
которое не имеет корней.
При 
получаем уравнение 
которое имеет единственный корень.
При 
получаем уравнение 
которое не имеет корней.
При 
и при 
исходное уравнение имеет единственный корень.
Ответ: 
| Критерии оценивания выполнения задания | Баллы |
|---|---|
| Обоснованно получен правильный ответ. | 4 |
| Получен верный ответ. Решение в целом верное. Обосновано найдены оба промежутка значений параметра из ответа к задаче, при этом возможны неточности с (не)включением концов и(или) вычислительная погрешность. | 3 |
| Обосновано найден хотя бы один промежуток значений параметра из ответа к задаче, при этом возможны неточности с (не)включением концов и(или) вычислительная погрешность. | 2 |
| Решение содержит: − или верное описание расположения двух лучей и прямой из условия задачи; − или верное получение квадратного уравнения с параметром a относительно одной из переменных. | 1 |
| Решение не соответствует ни одному из критериев, перечисленных выше. | 0 |
| Максимальный балл | 4 |