1. Тип 13 № 656542 
Классификатор алгебры: Уравнения смешанного типа, Тригонометрические уравнения, сводимые к целым на тангенс или котангенс
Методы алгебры: Введение замены
Уравнения. Тригонометрические уравнения, сводимые к квадратным
i
а) Решите уравнение 
б) Найдите все корни уравнения, принадлежащие отрезку 
Решение. а) Сделаем замену
заметим, что должно выполняться условие 
Преобразуем уравнение при этом условии:
Тогда
б) Для отбора корней воспользуемся тригонометрической окружностью (см. рис.). Подходят корни: 
Ответ: а)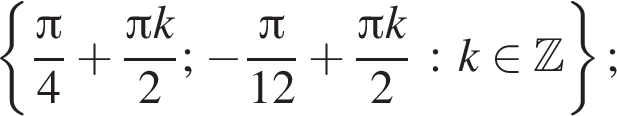 
б)
Критерии проверки:
| Критерии оценивания выполнения задания | Баллы |
|---|---|
| Обоснованно получены верные ответы в обоих пунктах | 2 |
| Обоснованно получен верный ответ в пункте а), ИЛИ получены неверные ответы из-за вычислительной ошибки, но при этом имеется верная последовательность всех шагов решения пункта а) и пункта б) | 1 |
| Решение не соответствует ни одному из критериев, перечисленных выше | 0 |
| Максимальный балл | 2 |
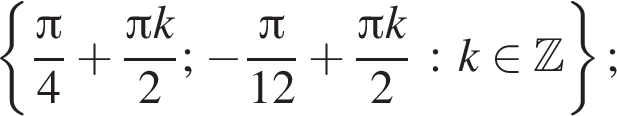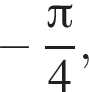
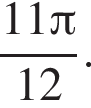
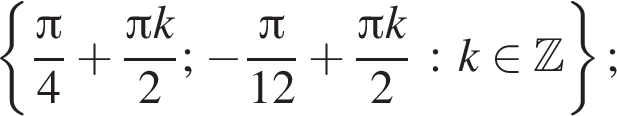Ответ: а) б)
б) 656542
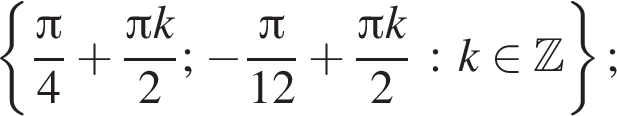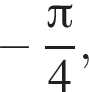
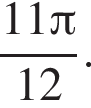
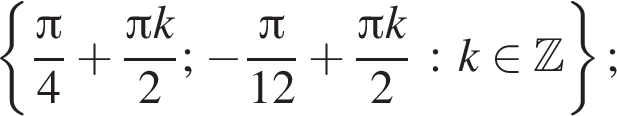а) б)
б) Классификатор алгебры: Уравнения смешанного типа, Тригонометрические уравнения, сводимые к целым на тангенс или котангенс
Методы алгебры: Введение замены
откуда
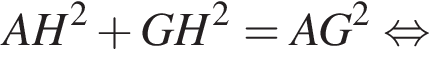
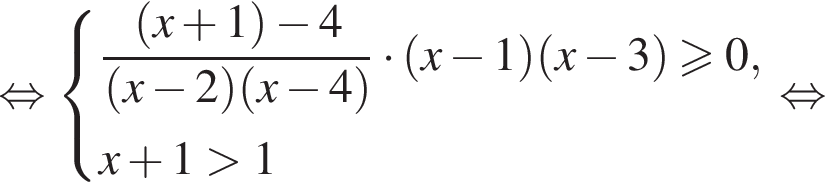
Тогда в новом сплаве массы металлов будут равны 
кг. Тогда
Оценим эту разность:
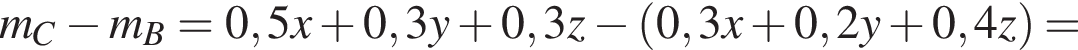
достигает наименьшего значения 
при 
Значит, чтобы условия задачи были выполнены, для получения нового сплава нужно использовать только первый и второй сплавы. Получаем систему
и 
В треугольник MNK вписан квадрат, две вершины которого лежат на стороне MN, одна на стороне NK и одна на стороне MK. Через середину стороны MN и центр квадрата проведена прямая, которая пресекается с высотой KH в точке O, а с прямой NK — в точке F.
Из подобия треугольников MNK и DCK получаем, что 
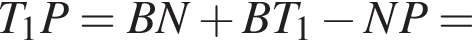
откуда
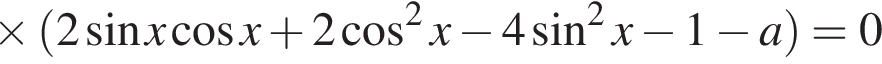
тоже являются корнями этого уравнения. Значит, исходное уравнение имеет ровно три различных корня, тогда и только тогда, когда уравнение (1) не имеет корней, а уравнение (2) имеет ровно три различных корня.
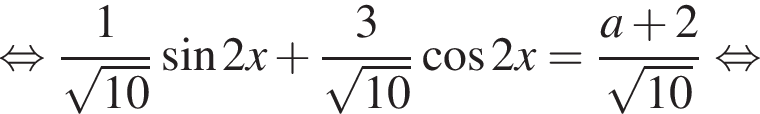
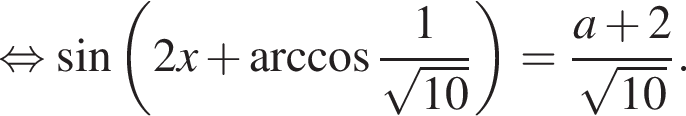
определенную на множестве действительных чисел, и исследуем её. Поведение на бесконечности:
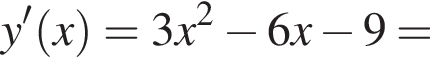
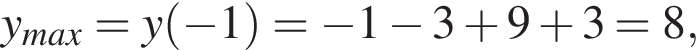
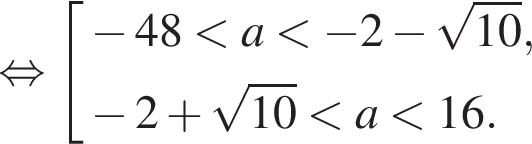
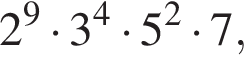то есть два числа, кратных 5, и еще одно, кратное 7 (чисел кратных одновременно 5 и 7 или кратных 52 у нас нет). В эти числа могут входить еще максимум 
множителя, равных 2 или 3 (если это числа 20, 
и 14). Поэтому остальные минимум 
таких множителей берутся из остальных трех чисел.
и ни одного, содержащего больше множителей. Значит, такое невозможно.
Таким образом, числитель будет содержать множители 11, 13, 17, 19 (останутся), 
(сократятся со знаменателем), и то ли 13 то ли 14 множителей, равных 2 и 3. 
невозможен. В самом деле, для этого в числителе нужно набрать 5 множителей 3. Среди чисел, кратных 5 или 7, такой множитель максимум один (если взять 15). Значит, среди остальных трех чисел этих множителей нужно минимум 4. При общем количестве множителей 2 и 3 среди этих чисел не меньше 10. Поэтому обязательно нужно взять число 16 и два числа из набора 8, 12, 18. Но среди них не получается выбрать четыре множителя 3. Осталось привести примеры для последних двух вариантов.
