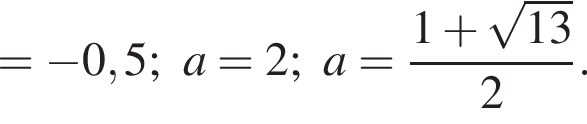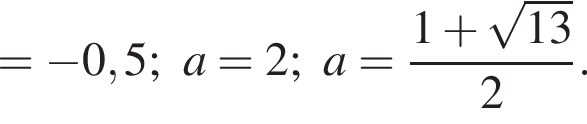Найдите все значения a, при каждом из которых уравнение
Решение. Преобразуем исходное уравнение:
Корнями этого уравнения являются корни уравнения
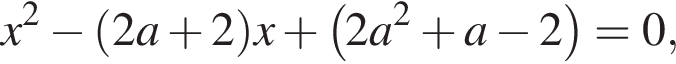
Если 
является корнем уравнения
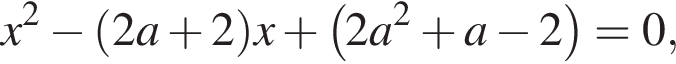
или 
Если 
является корнем уравнения
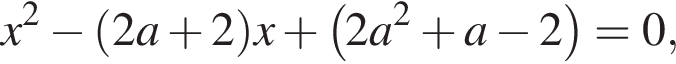
или 
Решим уравнение при полученных значениях a:
— при исходное уравнение имеет единственный корень 
— при 
исходное уравнение имеет единственный корень 
— при 
исходное уравнение имеет единственный корень 
Дискриминант квадратного уравнения
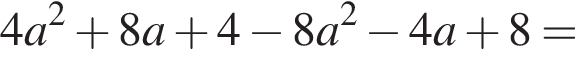
Значит, уравнение 
— имеет ровно два различных корня при 
— имеет ровно один корень пр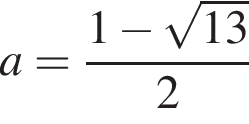и 
или 
— не имеет корней при 
или 
Таким образом, исходное уравнение имеет ровно один корень при
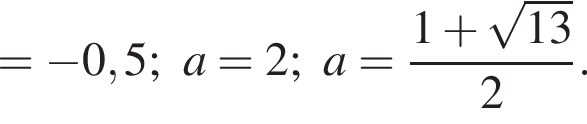
Ответ:
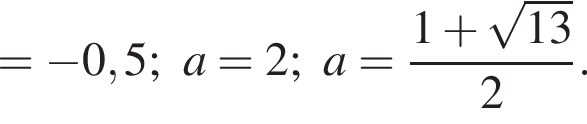
| Критерии оценивания выполнения задания | Баллы |
|---|---|
| Обоснованно получен верный ответ | 4 |
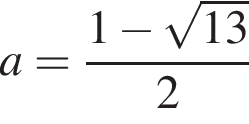С помощью верного рассуждения найдены точки  и множества значений a | 3 |
C помощью верного рассуждения найдены точки и  множества значений aИЛИ обоснованно получена хотя бы одна из точек множества значений a: | 2 |
| Задача верно сведена к исследованию корней уравнения
ИЛИ получен неверный ответ из-за вычислительной ошибки. но при этом верно выполнены все шаги решения | 1 |
| Решение не соответствует ни одному из критериев, перечисленных выше | 0 |
| Максимальный балл | 4 |
