i
Две окружности с центрами О1 и О2 соответственно касаются внешним образом. Из точки О1 проведена касательная О1К ко второй окружности (К — точка касания), а из точки О2 проведена касательная О2L к первой окружности (L — точка касания), точки К и L лежат по разные стороны от прямой О1О2.
а) Докажите, что 
б) Найдите радиус меньшей окружности, если дополнительно известно, что он в 

 Тогда четырехугольник O1KO2L вписан в окружность. Значит, углы
Тогда четырехугольник O1KO2L вписан в окружность. Значит, углы  равны как вписанные, опирающиеся на одну и ту же дугу.
равны как вписанные, опирающиеся на одну и ту же дугу.  и
и  Следовательно,
Следовательно, 

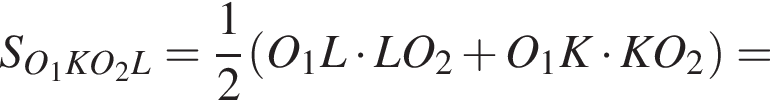





 откуда
откуда  то есть x = 3.
то есть x = 3.