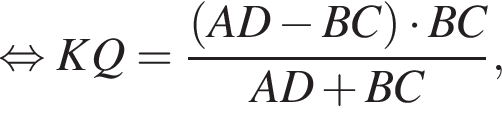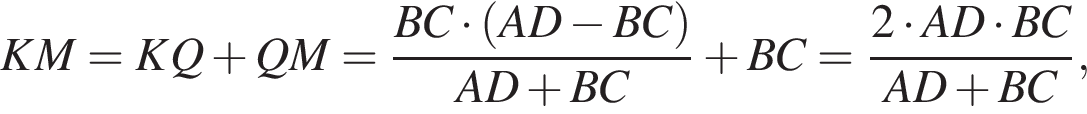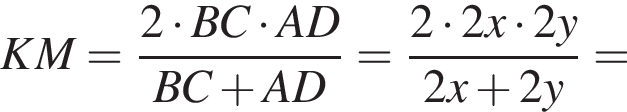i
Около окружности с центром O описана трапеция ABCD с основаниями AD и BC.
а) Докажите, что окружность, построенная на отрезке AB как на диаметре, проходит через точку O.
б) Найдите отношение площади четырёхугольника, вершины которого — точки касания окружности со сторонами трапеции, к площади самой трапеции ABCD, если известно, что AB = CD, а основания трапеции относятся как 3 : 4.




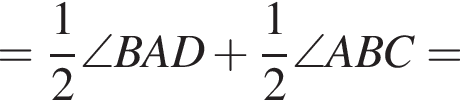







 Тогда
Тогда  LN = 2r —
LN = 2r —  Для полноты докажем это утверждение. Отложим на стороне AD отрезок PD = BC, и пусть Q — точка пересечения отрезков BP и KM. Тогда BCDP — параллелограмм и BP
Для полноты докажем это утверждение. Отложим на стороне AD отрезок PD = BC, и пусть Q — точка пересечения отрезков BP и KM. Тогда BCDP — параллелограмм и BP 

 QM = BC, а KQ находится из подобия треугольников BKQ и BAP:
QM = BC, а KQ находится из подобия треугольников BKQ и BAP: