РЕШУ ЕГЭ — математика профильная

Задания

Тип 19 № 561735 Добавить в вариант

Классификатор алгебры: Последовательности и прогрессии, Числа и их свойства, Числовые наборы на карточках и досках

Методы алгебры: Использование косвенных методов, Использование симметрий, оценок, монотонности

Числа и их свойства. Последовательности и прогрессии

На доске разрешается написать n таких ненулевых целых чисел a₁, a₂, ..., a_n, для которых при каждом натуральном числе k  =  2, ..., n − 1 выполнено равенство a_k  =  a_k − 1 + a_k + 1.

а)  Можно ли при n  =  4 написать на доске такие числа, чтобы также выполнялось равенство a₁  =  a₄?

б)  Можно ли при n  =  100 написать на доске такие числа, сумма которых равна 2021?

в)  При n  =  10 на доске написаны такие числа, сумма которых равна 11. Какое наименьшее значение может принимать сумма их квадратов?

Решение. а)  Пусть такие числа написаны. Поскольку по условию выполнены равенства $a_3=a_2 плюс a_4$ и $a_2=a_1 плюс a_3,$ получаем

$a_4=a_3 минус a_2= левая круглая скобка a_2 минус a_1 правая круглая скобка минус a_2= минус a_1.$

Следовательно, если также выполняется равенство $a_1=a_4,$ то $a_1=0.$ Пришли к противоречию.

б)  Пусть такие числа написаны. Поскольку при каждом натуральном числе $k=1,\dots,97$ по условию выполнены равенства $a_k плюс 2=a_k плюс 1 плюс a_k плюс 3$ и $a_k плюс 1=a_k плюс a_k плюс 2,$ получаем

$a_k плюс 3=a_k плюс 2 минус a_k плюс 1= левая круглая скобка a_k плюс 1 минус a_k правая круглая скобка минус a_k плюс 1= минус a_k,$ $a_k плюс 3=a_k плюс 2 минус a_k плюс 1=$
$= левая круглая скобка a_k плюс 1 минус a_k правая круглая скобка минус a_k плюс 1= минус a_k,$

и, следовательно,

$a_k плюс a_k плюс 1 плюс a_k плюс 2 плюс a_k плюс 3 плюс a_k плюс 4 плюс a_k плюс 5=0$ $a_k плюс a_k плюс 1 плюс a_k плюс 2 плюс$
$плюс a_k плюс 3 плюс a_k плюс 4 плюс a_k плюс 5=0$

при каждом натуральном числе $k=1,\dots,95.$ Значит,

$a_1 плюс a_2 плюс \dots плюс a_100=a_1 плюс a_2 плюс a_3 плюс a_4=a_2 плюс a_3.$ $a_1 плюс a_2 плюс \dots плюс a_100=$
$=a_1 плюс a_2 плюс a_3 плюс a_4=a_2 плюс a_3.$

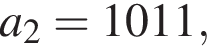
При $a_1=1,$ $a_2=1011,$ $a_3=1010$ и $a_k плюс 1=a_k минус 1 минус a_k$ при каждом натуральном числе $k=3,\dots,99$ имеем

$a_1 плюс a_2 плюс \dots плюс a_100=a_2 плюс a_3=2021.$

в)  Пусть такие числа написаны. Аналогично доказанному в п. б) получаем

$11=a_1 плюс a_2 плюс \dots плюс a_10=a_1 плюс a_2 плюс a_3 плюс a_4=a_2 плюс a_3.$ $11=a_1 плюс a_2 плюс \dots плюс a_10=$
$=a_1 плюс a_2 плюс a_3 плюс a_4=a_2 плюс a_3.$

С другой стороны,

$a_1 в квадрате плюс a_2 в квадрате плюс \dots плюс a_10 в квадрате =4a_1 в квадрате плюс 3 левая круглая скобка a_2 в квадрате плюс a_3 в квадрате правая круглая скобка =$
$=4 левая круглая скобка a_2 минус a_3 правая круглая скобка в квадрате плюс 3 левая круглая скобка a_2 в квадрате плюс a_3 в квадрате правая круглая скобка .$ $a_1 в квадрате плюс a_2 в квадрате плюс \dots плюс a_10 в квадрате =$
$=4a_1 в квадрате плюс 3 левая круглая скобка a_2 в квадрате плюс a_3 в квадрате правая круглая скобка =$
$=4 левая круглая скобка a_2 минус a_3 правая круглая скобка в квадрате плюс 3 левая круглая скобка a_2 в квадрате плюс a_3 в квадрате правая круглая скобка .$

Следовательно,

$a_1 в квадрате плюс a_2 в квадрате плюс \dots плюс a_10 в квадрате =7a_2 в квадрате минус 8a_2a_3 плюс 7a_3 в квадрате =$
$=7 левая круглая скобка a_2 плюс a_3 правая круглая скобка в квадрате минус 22a_2a_3=847 минус 22a_2a_3.$ $a_1 в квадрате плюс a_2 в квадрате плюс \dots плюс a_10 в квадрате =$
$=7a_2 в квадрате минус 8a_2a_3 плюс 7a_3 в квадрате =$
$=7 левая круглая скобка a_2 плюс a_3 правая круглая скобка в квадрате минус 22a_2a_3=847 минус 22a_2a_3.$ $a_1 в квадрате плюс a_2 в квадрате плюс \dots плюс a_10 в квадрате =$
$=7a_2 в квадрате минус 8a_2a_3 плюс 7a_3 в квадрате =$
$=7 левая круглая скобка a_2 плюс a_3 правая круглая скобка в квадрате минус 22a_2a_3=$
$=847 минус 22a_2a_3.$

Значит, сумма квадратов всех написанных чисел будет минимальна тогда и только тогда, когда максимально выражение $a_2a_3=a_2 левая круглая скобка 11 минус a_2 правая круглая скобка .$ Поскольку функция $f левая круглая скобка x правая круглая скобка =x левая круглая скобка 11 минус x правая круглая скобка$ возрастает при $x меньше или равно дробь: числитель: 11, знаменатель: 2 конец дроби$ и убывает при $x больше или равно дробь: числитель: 11, знаменатель: 2 конец дроби$ наибольшее значение выражения $a_2 левая круглая скобка 11 минус a_2 правая круглая скобка$ для целых $a_2$ равно 30. Оно достигается при $a_2=5$ и $a_2=6.$ Таким образом, получаем, что сумма

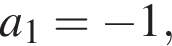
квадратов всех написанных чисел принимает наименьшее значение при $a_1= минус 1,$ $a_2=5,$ $a_3=6$ и $a_k плюс 1=a_k минус 1 минус a_k$ при каждом натуральном числе $k=3,\dots,9,$ а также при $a_1=1,$ $a_2=6,$ $a_3=5$ и $a_k плюс 1=a_k минус 1 минус a_k$ при каждом натуральном числе $k=3,\dots,9.$ Это значение равно

$847 минус 22a_2a_3=847 минус 660=187.$

Ответ: а)  нет; б)  да; в)  187.

Критерии проверки:

Критерии оценивания выполнения задания	Баллы
Получены верные обоснованные ответы в пунктах а, б и в	4
Получены верные обоснованные ответы в пунктах а и б, либо получены верные обоснованные ответы в пунктах а и в	3
Получен верный обоснованный ответ в пункте б, пункты а и в не решены, либо получен верный обоснованный ответ в пункте в, пункты а и б не решены	2
Приведён пример в пункте а, пункты б и в не решены	1
Решение не соответствует ни одному из критериев, перечисленных выше	0
Максимальный балл	4

Ответ: а)  нет; б)  да; в)  187.

561735

а)  нет; б)  да; в)  187.

Методы алгебры: Использование косвенных методов, Использование симметрий, оценок, монотонности

Ключ

№ п/п	№ задания	Ответ
1	561735	а)  нет; б)  да; в)  187.