Найдите все значения a, при каждом из которых для любой пары 
действительных чисел u и 
выполнено неравенство
Решение. Пусть
Имеем:
При фиксированных 
и a рассмотрим левую часть как функцию от x:
В зависимости от того, как располагается x относительно точек 
и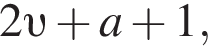 
модули раскроются по-разному. При этом на каждом участке непрерывная функция f(x) будет линейной с угловым коэффициентом 
Какова бы ни была комбинация знаков, 
Следовательно, f(x) монотонно возрастает. Поэтому неравенство 
выполняется при всех 
если и только если 
При малых 
то есть меньших, чем наименьшее из чисел 
и 
функция 
— возрастающая линейная с угловым коэффициентом 
При больших 
то есть больших, чем максимум из тех же чисел,
— убывающая линейная функция с угловым коэффициентом 
(см. рис.). Поэтому функция 
принимает наибольшее значение в одной из точек 
или 
Неравенство 
выполняется при всех тогда и только тогда, когда 
и 
Получаем:
Ответ: 
| Критерии оценивания выполнения задания | Баллы |
|---|---|
| Обоснованно получен правильный ответ. | 4 |
| С помощью верного рассуждения получены оба верных значения параметра, но – или в ответ включены также и одно-два неверных значения; – или решение недостаточно обосновано. | 3 |
| С помощью верного рассуждения получено хотя бы одно верное значение параметра. | 2 |
| Задача сведена к исследованию: – или взаимного расположения трёх окружностей; – или двух квадратных уравнений с параметром. | 1 |
| Решение не соответствует ни одному из критериев, перечисленных выше. | 0 |