РЕШУ ЕГЭ — математика профильная

Задания

Найдите все значений a, при каждом из которых система уравнений

$система выражений левая круглая скобка y в квадрате минус xy плюс x минус 3y плюс 2 правая круглая скобка корень из: начало аргумента: x плюс 3 конец аргумента =0,a минус x минус y=0 конец системы .$

имеет ровно два различных решения.

Решение. Преобразуем первое уравнение системы:

$левая круглая скобка y в квадрате минус xy плюс x минус 3y плюс 2 правая круглая скобка корень из: начало аргумента: x плюс 3 конец аргумента =0 равносильно$
$равносильно левая круглая скобка y минус 1 правая круглая скобка левая круглая скобка y минус x минус 2 правая круглая скобка корень из: начало аргумента: x плюс 3 конец аргумента =0 равносильно$

$равносильно система выражений совокупность выражений y=x плюс 2,y=1,x= минус 3, конец системы .x \geqslant минус 3. конец совокупности .$

Исходная система имеет ровно два различных решения тогда и только тогда, когда графики функций $y=x плюс 2$ и $y=1$ и прямая $x= минус 3$ имеют с прямой $y= минус x плюс a$ две различных точки пересечения на области $x больше или равно минус 3$ (см. рис.).

Из рисунка видно, что

—  при $a\leqslant минус 4$ система имеет одно решение;

—  при $минус 4 меньше a\leqslant минус 2$   — два решения;

—  при $минус 2 меньше a меньше 0$   — три решения;

—  при $a=0$   — два решения;

—  при $a больше 0$   — три решения.

Ответ: $минус 4 меньше a\leqslant минус 2;$ $a=0.$

Приведём другое (аналитическое) решение.

Запишем первое уравнение в виде 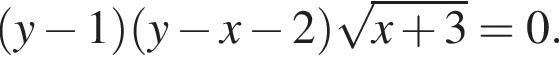$левая круглая скобка y минус 1 правая круглая скобка левая круглая скобка y минус x минус 2 правая круглая скобка корень из: начало аргумента: x плюс 3 конец аргумента =0.$ Решения первого уравнения системы совпадают с решениями уравнений $y=1,$ $y=x плюс 2$ и $x= минус 3$ при условии $x\geqslant минус 3.$

При $x= минус 3$ уравнение $a минус x минус y=0$ имеет единственное решение при любом значении a.

При $y=1$ уравнение $a минус x минус y=0$ принимает вид $a минус x минус 1=0,$ откуда $x=a минус 1.$ C учётом условия $x\geqslant минус 3$ получаем, что при $a меньше минус 2$ решений нет, а при $a\geqslant минус 2$ имеется одно решение.

При $y=x плюс 2$ уравнение $a минус x минус y=0$ принимает вид $a минус x минус x минус 2=0,$ откуда $x= дробь: числитель: a, знаменатель: 2 конец дроби минус 1.$ C учётом условия $x\geqslant минус 3$ получаем, что при $a меньше минус 4$ решений нет, а при $a\geqslant минус 4$ имеет одно решение.

Определим значения a, при которых возможны совпадения решений из трёх разобранных выше случаев. Имеем: либо $x= минус 3,$ $y=1,$ откуда $a= минус 2;$ либо $x= минус 3,$ $y=x плюс 2= минус 1,$ откуда $a= минус 4;$ либо $y=1,$ $y=x плюс 2,$ откуда $x= минус 1,$ $a=0.$

Таким образом, исходная система имеет единственное решение при $a\leqslant минус 4,$ имеет два решения при $минус 4 меньше a\leqslant минус 2$ и $a=0,$ имеет три решения при $минус 2 меньше a меньше 0$ и $a больше 0.$

Ответ: $минус 4 меньше a\leqslant минус 2;$ $a=0.$

Критерии оценивания выполнения задания	Баллы
Обоснованно получен верный ответ	4
С помощью верного рассуждения получено множество значений a, отличающееся от искомого только включением/⁠исключением точек 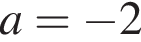$a= минус 4$ и/или $a= минус 2$	3
C помощью верного рассуждения получен промежуток $левая круглая скобка минус 4; минус 2 правая круглая скобка$ множества значений a, возможно, с включением/⁠исключением граничных точек	2
Верно найдено хотя бы одно из значений a: 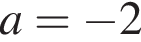$a= минус 2$ или $a=0;$ ИЛИ получен неверный ответ из-за вычислительной ошибки, но при этом верно выполнены все шаги решения	1
Решение не соответствует ни одному из критериев, перечисленных выше	0
Максимальный балл	4

№ п/п	№ задания	Ответ
1	514387	$минус 4 меньше a\leqslant минус 2;$ $a=0.$

Ключ