РЕШУ ЕГЭ — математика профильная

Задания

Тип 18 № 511452 Добавить в вариант

Классификатор алгебры: Функции, зависящие от параметра

Методы алгебры: Группировка

Задача с параметром. Функции, зависящие от параметра

Найдите все значения a, при каждом из которых наименьшее значение функции

$f левая круглая скобка x правая круглая скобка =6ax плюс \left| x в квадрате минус 6x . плюс 5 |$

больше, чем $минус 24.$

Решение. 1.  При $x в квадрате минус 6x плюс 5= левая круглая скобка x минус 1 правая круглая скобка левая круглая скобка x минус 5 правая круглая скобка меньше или равно 0 равносильно x принадлежит левая квадратная скобка 1,5 правая квадратная скобка$ функция имеет вид:

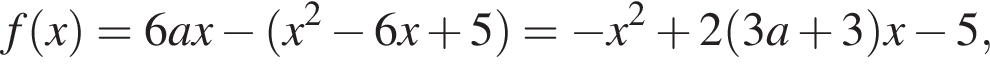
$f левая круглая скобка x правая круглая скобка =6ax минус левая круглая скобка x в квадрате минус 6x плюс 5 правая круглая скобка = минус x в квадрате плюс 2 левая круглая скобка 3a плюс 3 правая круглая скобка x минус 5,$ $f левая круглая скобка x правая круглая скобка =6ax минус левая круглая скобка x в квадрате минус 6x плюс 5 правая круглая скобка =$
$= минус x в квадрате плюс 2 левая круглая скобка 3a плюс 3 правая круглая скобка x минус 5,$

а её график представляет собой часть параболы с ветвями, направленными вниз.

При $x в квадрате минус 6x плюс 5= левая круглая скобка x минус 1 правая круглая скобка левая круглая скобка x минус 5 правая круглая скобка больше или равно 0 равносильно x принадлежит левая круглая скобка минус бесконечность ,1 правая квадратная скобка \cup левая квадратная скобка 5, плюс бесконечность правая круглая скобка$ функция имеет вид:

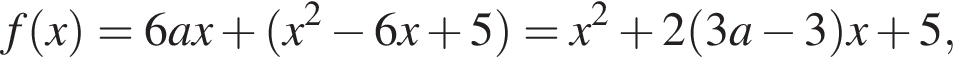
$f левая круглая скобка x правая круглая скобка =6ax плюс левая круглая скобка x в квадрате минус 6x плюс 5 правая круглая скобка =x в квадрате плюс 2 левая круглая скобка 3a минус 3 правая круглая скобка x плюс 5,$ $f левая круглая скобка x правая круглая скобка =6ax плюс левая круглая скобка x в квадрате минус 6x плюс 5 правая круглая скобка =$
$=x в квадрате плюс 2 левая круглая скобка 3a минус 3 правая круглая скобка x плюс 5,$

а ее график состоит из двух частей параболы с ветвями, направленными вверх и осью симметрии $x=3 минус 3a.$

2.  Если $3 минус 3a$ принадлежит отрезку $левая квадратная скобка 1,5 правая квадратная скобка ,$ то наименьшее значение функция может принимать только в точках $x=1$ и $x=5.$ Если $3 минус 3a принадлежит левая круглая скобка минус бесконечность ,1 правая квадратная скобка \cup левая квадратная скобка 5, плюс бесконечность правая круглая скобка$   — то еще и в точке $x=3 минус 3a.$

3.  Наименьшее значение функции $f левая круглая скобка x правая круглая скобка$ больше $минус 24$ тогда и только тогда, когда либо

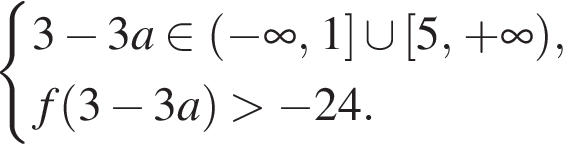
$система выражений новая строка 3 минус 3a принадлежит левая квадратная скобка 1,5 правая квадратная скобка , новая строка f левая круглая скобка 1 правая круглая скобка больше минус 24, новая строка f левая круглая скобка 5 правая круглая скобка больше минус 24, конец системы .$ либо $система выражений новая строка 3 минус 3a принадлежит левая круглая скобка минус бесконечность ,1 правая квадратная скобка \cup левая квадратная скобка 5, плюс бесконечность правая круглая скобка , новая строка f левая круглая скобка 3 минус 3a правая круглая скобка больше минус 24. конец системы .$

Решим первую систему:

$система выражений новая строка минус дробь: числитель: 2, знаменатель: 3 конец дроби меньше или равно a меньше или равно дробь: числитель: 2, знаменатель: 3 конец дроби , новая строка 6a больше минус 24, новая строка 30a больше минус 24 конец системы . равносильно a принадлежит левая квадратная скобка минус дробь: числитель: 2, знаменатель: 3 конец дроби , дробь: числитель: 2, знаменатель: 3 конец дроби правая квадратная скобка .$

Решим вторую систему:

$система выражений новая строка a принадлежит левая круглая скобка минус бесконечность , минус дробь: числитель: 2, знаменатель: 3 конец дроби правая круглая скобка \cup левая круглая скобка дробь: числитель: 2, знаменатель: 3 конец дроби , плюс бесконечность правая круглая скобка , новая строка \left| 3a минус 3 | . меньше корень из: начало аргумента: 29 конец аргумента конец системы . равносильно$
$равносильно a принадлежит левая круглая скобка дробь: числитель: 3 минус корень из: начало аргумента: 29 конец аргумента , знаменатель: 3 конец дроби , минус дробь: числитель: 2, знаменатель: 3 конец дроби правая круглая скобка \cup левая круглая скобка дробь: числитель: 2, знаменатель: 3 конец дроби , дробь: числитель: 3 плюс корень из: начало аргумента: 29 конец аргумента , знаменатель: 3 конец дроби правая круглая скобка .$

Ответ: $\a принадлежит левая круглая скобка дробь: числитель: 3 минус корень из: начало аргумента: 29 конец аргумента , знаменатель: 3 конец дроби , дробь: числитель: 3 плюс корень из: начало аргумента: 29 конец аргумента , знаменатель: 3 конец дроби правая круглая скобка .$

Критерии проверки:

Критерии оценивания выполнения задания	Баллы
Обоснованно получен верный ответ	4
С помощью верного рассуждения получены все верные значения параметра, но решение недостаточно обосновано	3
С помощью верного рассуждения получен промежуток, содержащий верный ответ, либо содержащийся в верном промежутке	2
Задача сведена к исследованию взаимного расположения частей двух парабол	1
Решение не соответствует ни одному из критериев, перечисленных выше	0
Максимальный балл	4

511452

$\a принадлежит левая круглая скобка дробь: числитель: 3 минус корень из: начало аргумента: 29 конец аргумента , знаменатель: 3 конец дроби , дробь: числитель: 3 плюс корень из: начало аргумента: 29 конец аргумента , знаменатель: 3 конец дроби правая круглая скобка .$

Классификатор алгебры: Функции, зависящие от параметра

Методы алгебры: Группировка

Ключ

№ п/п	№ задания	Ответ
1	511452	$\a принадлежит левая круглая скобка дробь: числитель: 3 минус корень из: начало аргумента: 29 конец аргумента , знаменатель: 3 конец дроби , дробь: числитель: 3 плюс корень из: начало аргумента: 29 конец аргумента , знаменатель: 3 конец дроби правая круглая скобка .$