Найдите все значения a, при каждом из которых уравнение
Решение. Запишем уравнение в виде 
Рассмотрим две функции: 
и 
Графиком функции является полуокружность радиуса 
с центром в точке 
лежащая в верхней полуплоскости. При каждом значении a графиком функции 
является прямая с угловым коэффициентом 
проходящая через точку 
Уравнение имеет единственный корень, если графики функций 
и имеют единственную общую точку: либо прямая касается полуокружности, либо пересекает её в единственной точке.
Касательная MC, проведённая из точки M к полуокружности, имеет угловой коэффициент, равный нулю, то есть при 
исходное уравнение имеет единственный корень. При 
прямая не имеет общих точек с полуокружностью.
Прямая MB, заданная уравнением 
проходит через точки 
и 
следовательно, её угловой коэффициент 
При 
прямая, заданная уравнением 
имеет угловой коэффициент не меньше, чем у прямой MB, и пересекает полуокружность в двух точках.
Прямая MA, заданная уравнением проходит через точки и 
следовательно, её угловой коэффициент 
При 
прямая, заданная уравнением 
имеет угловой коэффициент не меньше, чем у прямой MA, и меньше, чем у прямой MB, и пересекает полуокружность в единственной точке. Получаем, что при 
исходное уравнение имеет единственный корень.
Ответ: 
| Критерии оценивания выполнения задания | Баллы |
|---|---|
| Обоснованно получен правильный ответ | 4 |
Обоснованно получены все значения:  Ответотличается от верного только исключением точки | 3 |
Обоснованно получены все значения:  | 2 |
Верно найдено одно или два из значений  или | 1 |
| Решение не соответствует ни одному из критериев, перечисленных вышe | 0 |
| Максимальный балл | 4 |
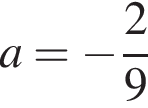и/или включением точки 