Угол C треугольника ABC равен 
D — отличная от A точка пересечения окружностей, построенных на сторонах AB и AC как на диаметрах. Известно, что 
Найдите угол 
Решение. Точка D лежит на окружности с диаметром AB, поэтому
Аналогично,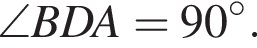 
Следовательно, точка D лежит на прямой 
Из прямоугольных треугольников ADC и ADB находим:
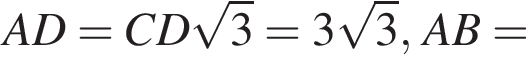
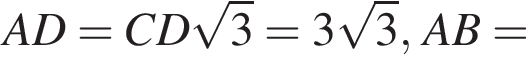
Возможны два случая.
Первый случай. Точка D лежит на отрезке BC (рис. 1). По теореме синусов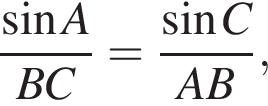 
то есть 
откуда 
Второй случай. Точка D лежит на продолжении отрезка BC за точку B (рис. 2). Точка D не может лежать на продолжении отрезка BC за точку C, так как угол ACB — острый.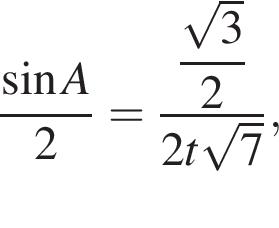 
откуда 
Поскольку 
получаем: 
значит, 
— острый и равен 
или 
Ответ: 
| Критерии оценивания выполнения задания | Баллы |
|---|---|
| Рассмотрены все возможные геометрические конфигурации и получен правильный ответ | 3 |
| Рассмотрена хотя бы одна возможная конфигурация, в которой получено правильное значение искомой величины | 2 |
| Рассмотрена хотя бы одна возможная геометрическая конфигурация, в которой получено значение искомой величины, неправильное из-за арифметической ошибки | 1 |
| Решение не соответствует ни одному из критериев, перечисленных выше | 0 |
| Максимальный балл | 3 |