Окружность S проходит через вершину C прямого угла и пресекает его стороны в точках, удаленных от вершины C на расстояния 12 и 16. Найдите радиус окружности, вписанной в данный угол и касающийся окружности S.
Решение. Пусть окружность S с центром O и радиусом R пересекает стороны данного прямого угла в точках A и B,
искомая окружность с центром Q касается сторон и BC угла ACB в точках N и K соответственно, а окружности S — в точке 
Точка O — центр окружности, описанной около прямоугольного треугольника ABC, поэтому O — середина его гипотенузы 
Тогда
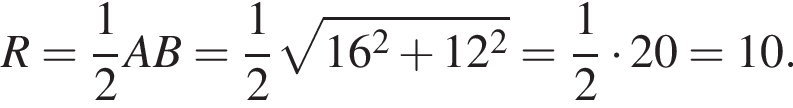
Линия центров двух касающихся окружностей проходит через точку их касания, поэтому точки M, O и Q лежат на одной прямой. Опустим перпендикуляр OH из центра окружности S на прямую 
Тогда OH — средняя линия треугольника ABC поэтому 
и 
а так как центр окружности, вписанной в угол, лежит на его биссектрисе, то 
поэтому 
Опустим перпендикуляр QF из центра искомой окружности на прямую 
Тогда
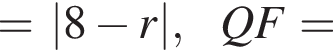
Предположим, что искомая окружность и окружность касаются внутренним образом. Тогда
Рассмотрим прямоугольный треугольник 
По теореме Пифагора 
или
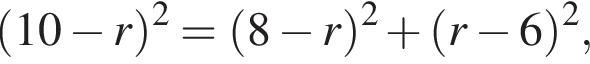откуда находим, что 
Если же искомая окружность касается данной внешним образом, то
Тогда из соответствующего уравнения 
находим, что 
Ответ: 8 или 48.
| Критерии оценивания выполнения задания | Баллы |
|---|---|
| Рассмотрены все возможные геометрические конфигурации, и получен правильный ответ | 3 |
| Рассмотрена хотя бы одна возможная конфигурация, в которой получено правильное значение искомой величины | 2 |
| Рассмотрена хотя бы одна возможная геометрическая конфигурация, в которой получено значение искомой величины, неправильное из-за геометрической ошибки | 1 |
| Решение не соответствует ни одному из критериев, перечисленных выше | 0 |
| Максимальный балл | 3 |