Тип Д15 C4 № 511226 
Сложная планиметрия. Треугольники
i
а) Докажите, что в прямоугольном треугольнике сумма длин диаметров вписанной и описанной окружностей равна сумме длин катетов.
б) В прямоугольном треугольнике ABC из вершины прямого угла проведена высота CH. Найдите сумму длин радиусов окружностей, вписанных в треугольники ABC, ACH и BCH, если известно, что 
Решение. 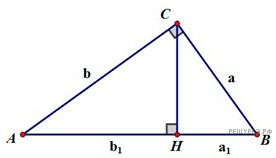 а) Пусть катеты заданного прямоугольного треугольника ABC равны a и b, гипотенуза равна c. Прежде докажем, что радиус r окружности, вписанной в этот треугольник, может быть вычислен по формуле
а) Пусть катеты заданного прямоугольного треугольника ABC равны a и b, гипотенуза равна c. Прежде докажем, что радиус r окружности, вписанной в этот треугольник, может быть вычислен по формуле  Будем рассуждать так:
Будем рассуждать так:
Известно, что

Если нам удастся доказать, что выполняется равенство  для заданного треугольника, то цель будет достигнута.
для заданного треугольника, то цель будет достигнута.





(последнее равенство верно для любого прямоугольного треугольника). Следовательно, радиус вписанной окружности равен  Тогда диаметр этой окружности d = a + b − c.
Тогда диаметр этой окружности d = a + b − c.
Как известно, диаметр окружности D, описанной около треугольника ABC, будет равен его гипотенузе, т. е. с.
Таким образом, d + D = a + b − c + c = a + b, что и требовалось доказать.
б) Пусть AC = b, BC = a, AH = b1, BH = a1, CH = h; rc, rb, ra — радиусы окружностей, вписанных в треугольники ABC, ACH и BCH соответственно. Тогда по сказанному выше:


Ответ: б) 
Критерии проверки:| Критерии оценивания выполнения задания | Баллы |
|---|
| Имеется верное доказательство утверждения пункта а и обоснованно получен верный ответ в пункте б. | 3 |
| Получен обоснованный ответ в пункте б. ИЛИ Имеется верное доказательство утверждения пункта а и при обоснованном решении пункта б получен неверный ответ из-за арифметической ошибки. | 2 |
| Имеется верное доказательство утверждения пункта а. ИЛИ При обоснованном решении пункта б получен неверный ответ из-за арифметической ошибки. ИЛИ Обоснованно получен верный ответ в пункте б и использованием утверждения пункта а, при этом пункт а не выполнен. | 1 |
| Решение не соответствует ни одному из критериев, перечисленных выше. | 0 |
| Максимальный балл | 3 |
Ответ: б)

511226
б)

 PDF-версии:
PDF-версии: 