
Найдите все значения a, при которых неравенство 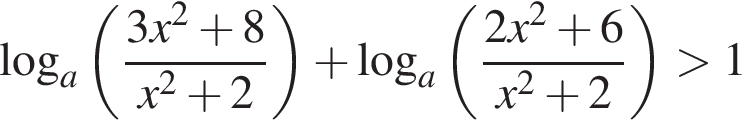 не имеет решений.
не имеет решений.
Решение. Неравенство не имеет смысла при неположительных значениях параметра и при ![]() и, поэтому не имеет решений при указанных
и, поэтому не имеет решений при указанных ![]()
Заметим, что


Положим  Ввиду того, что
Ввиду того, что  множество значений выражения
множество значений выражения  при
при ![]() является промежуток
является промежуток ![]() Значит, неравенство
Значит, неравенство 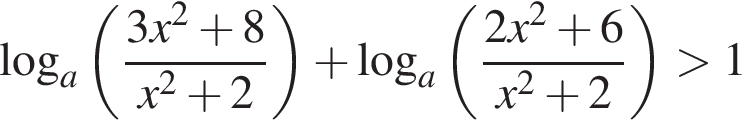 не имеет решений тогда и только тогда, когда на промежутке
не имеет решений тогда и только тогда, когда на промежутке ![]() не имеет решений неравенство
не имеет решений неравенство 
Имеем:
1) при  неравенство
неравенство ![]() не имеет решений на промежутке
не имеет решений на промежутке ![]() так как на этом промежутке оба слагаемых левой части неравенства отрицательны;
так как на этом промежутке оба слагаемых левой части неравенства отрицательны;
2) при ![]() неравенство
неравенство ![]() равносильно неравенству
равносильно неравенству 
Функция  должна быть неположительна на промежутке
должна быть неположительна на промежутке ![]() значит, её график должен быть расположен не выше интервала
значит, её график должен быть расположен не выше интервала ![]() оси абсцисс, то есть, должно выполняться условие
оси абсцисс, то есть, должно выполняться условие  Решая неравенство
Решая неравенство  получаем
получаем 
Ответ: 
Замечание.
Пункт 2) можно выполнить иначе с помощью следующих рассуждений:
Поскольку вершина параболы  имеет координаты
имеет координаты  функция
функция  возрастает на промежутке
возрастает на промежутке ![]() и, значит, множеством ее значений на этом промежутке является промежуток
и, значит, множеством ее значений на этом промежутке является промежуток  , то есть промежуток
, то есть промежуток  Таким образом, неравенство
Таким образом, неравенство  неверно для всех t из промежутка
неверно для всех t из промежутка ![]() в том и только в том случае, когда выполняется условие
в том и только в том случае, когда выполняется условие 
| Критерии оценивания выполнения задания | Баллы |
|---|---|
| Обоснованно получен правильный ответ. | 4 |
| Обосновано получен ответ отличающийся от верного только исключением и/или включением ГРАНИЧНЫХ точек ИЛИ Ответ неверен вследствие одной вычислительной ошибки (описки), не повлиявшей на ход решения и не упростившей задачу. | 3 |
| С помощью верного рассуждения получены искомые значения | 2 |
Задача сведена к исследованию взаимного расположения графика функции и отрезка (2; 3] или (при аналитическом решении) найдено множество значений функции  но дальнейшие рассуждения неверны или отсутствуют. но дальнейшие рассуждения неверны или отсутствуют. | 1 |
| Решение не соответствует ни одному из критериев, перечисленных выше. | 0 |