РЕШУ ЕГЭ — математика профильная

Задания

Тип 1 № 30635 Добавить в вариант

Кодификатор ФИПИ/Решу ЕГЭ:

1.2.1 Синус, косинус, тангенс, котангенс произвольного угла;

5.1.1 Треугольник.

Планиметрия. Решение прямоугольного треугольника

В треугольнике ABC угол C равен 90°, CH  — высота, 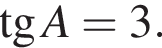$AB = 5,$ $тангенс A = 3.$ Найдите BH.

Решение.

Это задание ещё не решено, приводим решение прототипа.

В треугольнике АВС угол С равен 90°, СН  — высота, $AB = 13,$ $тангенс A = 5.$ Найдите ВН.

Углы А и НСВ равны как острые углы со взаимно перпендикулярными сторонами.

$BH=CB синус \widehatHCB=CB синус A=$
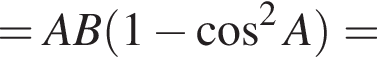
$=AB синус в квадрате A=AB левая круглая скобка 1 минус косинус в квадрате A правая круглая скобка =$ $BH=CB синус \widehatHCB=$
$=CB синус A=AB синус в квадрате A=$
$=AB левая круглая скобка 1 минус косинус в квадрате A правая круглая скобка =$ $AB левая круглая скобка 1 минус дробь: числитель: 1, знаменатель: 1 плюс tg в квадрате A конец дроби правая круглая скобка =13 левая круглая скобка 1 минус дробь: числитель: 1, знаменатель: 26 конец дроби правая круглая скобка =12,5.$

Ответ: 12,5.

Приведем решение Александра Широкова.

Пусть BH  =  x, тогда AH  =  13 − x. Из прямоугольного треугольника ACH находим:

$CH=AH тангенс A= левая круглая скобка 13 минус x правая круглая скобка тангенс A.$

Углы А и НСВ равны как острые углы со взаимно перпендикулярными сторонами, следовательно, из прямоугольного треугольника HCB имеем:

$CH= дробь: числитель: BH, знаменатель: тангенс A конец дроби = дробь: числитель: x, знаменатель: тангенс A конец дроби .$

Приравняв правые части полученных выражений, получим:

$5 левая круглая скобка 13 минус x правая круглая скобка = дробь: числитель: x, знаменатель: 5 конец дроби равносильно 26 x=325 равносильно x=12,5.$

Приведем решение Tema Resa.

Заметим, что $тангенс A= дробь: числитель: BC, знаменатель: AC конец дроби ,$ откуда $BC=5AC.$ По теореме Пифагора $AC в квадрате плюс BC в квадрате =AB в квадрате ,$ следовательно,

$AC в квадрате плюс левая круглая скобка 5AC правая круглая скобка в квадрате =13 в квадрате равносильно AC= корень из: начало аргумента: 6,5 конец аргумента .$

Из прямоугольного треугольника ABC $косинус A= дробь: числитель: AC, знаменатель: AB конец дроби = дробь: числитель: корень из: начало аргумента: 6,5 конец аргумента , знаменатель: 13 конец дроби = дробь: числитель: 1, знаменатель: корень из: начало аргумента: 26 конец аргумента конец дроби .$ Из прямоугольного треугольника ACH получим:

$косинус A = дробь: числитель: AH, знаменатель: AC конец дроби равносильно$
$равносильно AH=AC умножить на косинус A = корень из: начало аргумента: 6,5 конец аргумента умножить на дробь: числитель: 1, знаменатель: корень из: начало аргумента: 26 конец аргумента конец дроби = корень из: начало аргумента: дробь: числитель: 1, знаменатель: 4 конец дроби конец аргумента =0,5.$

Тогда $BH=AB минус AH=13 минус 0,5=12,5.$

Кодификатор ФИПИ/Решу ЕГЭ:

1.2.1 Синус, косинус, тангенс, котангенс произвольного угла;

5.1.1 Треугольник.

Ключ